




 For
a structure this size you would need thicker tubing, so it utilizes
top rail such as is used along the tops of chain link fences.
For
a structure this size you would need thicker tubing, so it utilizes
top rail such as is used along the tops of chain link fences.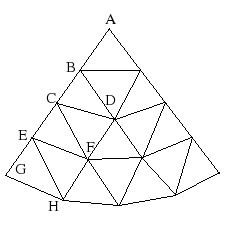
|
point
|
height
|
ht. for 14'
|
|
A
|
1.0000
|
14.00
|
|
B
|
0.9375
|
13.125
|
|
C
|
0.7500
|
10.5
|
|
D
|
0.7500
|
10.5
|
|
E
|
0.4375
|
6.125
|
|
F
|
0.4375
|
6.125
|
|
G,H,I
|
0.0000
|
0.00
|
|
Strut Name
|
Chord Factor
|
Center-center
for 14' height
|
Center-center
plus 0.1 feet
|
|
AB
|
0.25769
|
3.6077
|
3.7077
|
|
BB
|
0.25000
|
3.5000
|
3.6000
|
|
BC
|
0.31250
|
4.3750
|
4.4750
|
|
BD
|
0.36214
|
5.0700
|
5.1700
|
|
CE
|
0.40020
|
5.6027
|
5.7027
|
|
CF
|
0.45320
|
6.3447
|
6.4447
|
|
CD
|
0.25882
|
3.6235
|
3.7235
|
|
DF
|
0.41419
|
5.7986
|
5.8986
|
|
EF
|
0.26047
|
3.6466
|
3.7466
|
|
EG
|
0.50389
|
7.0545
|
7.1545
|
|
EH
|
0.55228
|
7.7320
|
7.8320
|
|
FF
|
0.26047
|
3.6466
|
3.7466
|
|
FH
|
0.50952
|
7.1333
|
7.2333
|
|
FI
|
0.52602
|
7.3642
|
7.4642
|
|
GH,HI
|
0.26105
|
3.6547
|
3.7547
|
 A
number of years ago I made a structure 20’ square by 5’
deep out of top rail used for chain link fences. I used this to cover
the space between our back porch and a small shop. I covered it with
chicken wire, which supported 6-mil plastic, which was in turn
covered by another layer of chicken wire to keep the wind from
removing the plastic.
A
number of years ago I made a structure 20’ square by 5’
deep out of top rail used for chain link fences. I used this to cover
the space between our back porch and a small shop. I covered it with
chicken wire, which supported 6-mil plastic, which was in turn
covered by another layer of chicken wire to keep the wind from
removing the plastic.
|
Point
|
Height
|
Chord
|
Chord Factor
|
|
|
A
|
1
|
AB
|
.16890
|
|
|
B
|
0.9722
|
BB
|
.16667
|
|
|
C
|
0.8889
|
BC
|
.18634
|
|
|
D
|
0.8889
|
BD
|
.22272
|
|
|
E
|
0.7500
|
CD
|
.17255
|
|
|
F
|
0.7500
|
CE
|
.21695
|
|
|
G
|
0.5556
|
CF
|
.25916
|
|
|
H
|
0.5556
|
DF
|
.22832
|
|
|
I
|
0.5556
|
EF
|
.17365
|
|
|
J
|
0.3056
|
FF
|
.17365
|
|
|
K
|
0.3056
|
EG
|
.25610
|
|
|
L
|
0.3056
|
EH
|
.29715
|
|
|
M
|
0
|
FH
|
.26100
|
|
|
N
|
0
|
FI
|
.27516
|
|
|
O
|
0
|
GH
|
.17403
|
|
|
P
|
0
|
HI
|
.17403
|
|
|
|
|
GJ
|
.30046
|
|
|
|
|
GK
|
.33846
|
|
|
|
|
HK
|
.30298
|
|
|
|
|
HL
|
.32242
|
|
|
|
|
IL
|
.31042
|
|
|
|
|
JK
|
.17421
|
|
|
|
|
KL
|
.17421
|
|
|
|
|
LL
|
.17421
|
|
|
|
|
JM
|
.34805
|
|
|
|
|
JN
|
.38270
|
|
|
|
|
KN
|
.34951
|
|
|
|
|
KO
|
.37082
|
|
|
|
|
LO
|
.35384
|
|
|
|
|
LP
|
.36093
|
|
|
|
|
MN
|
.71431
|
|
|
|
|
NO
|
.17431
|
|
|
|
|
OP
|
.17431
|
|
|
|
|
|
|
|
|
A
|
|
|
|
|
|
|
|
B
|
|
B
|
|
|
|
|
|
C
|
|
D
|
|
|
|
|
|
E
|
|
F
|
|
F
|
|
|
|
G
|
|
H
|
|
I
|
|
|
|
J
|
|
K
|
|
L
|
|
L
|
|
M
|
|
N
|
|
O
|
|
P
|
|